In 1952 David Huffman, a graduate student at the famous Massachusetts Institute of Technology developed an elegant algorithm for lossless compression as part of his schoolwork. The algorithm is now known as Huffman coding.
Huffman coding can be used to compress all sorts of data. It is an entropy-based algorithm that relies on an analysis of the frequency of symbols in an array.
Huffman coding can be demonstrated most vividly by compressing a raster image. Suppose we have a 5x5 raster image with 8-bit color, i.e. 256 different colors. The uncompressed image will take 5 x 5 x 8 = 200 bits of storage.

First, we count up how many times each color occurs in the image. Then we sort the colors in order of decreasing frequency. We end up with a row that looks like this:

Now we put the colors together by building a tree such that the colors farthest from the root are the least frequent. The colors are joined in pairs, with a node forming the connection. A node can connect either to another node or to a color. In our example, the tree might look like this:
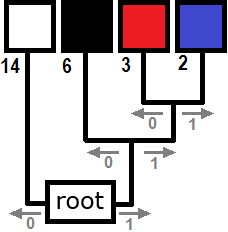
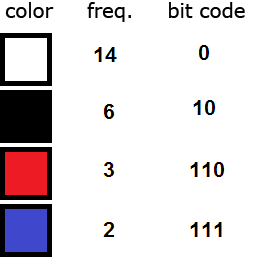
Our result is known as a Huffman tree. It can be used for encoding and decoding. Each color is encoded as follows. We create codes by moving from the root of the tree to each color. If we turn right at a node, we write a 1, and if we turn left - 0. This process yields a Huffman code table in which each symbol is assigned a bit code such that the most frequently occurring symbol has the shortest code, while the least common symbol is given the longest code.
The Huffman tree and code table we created are not the only ones possible. An alternative Huffman tree that looks like this could be created for our image:
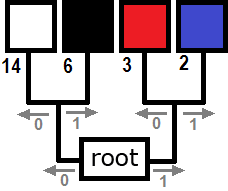
The corresponding code table would then be:
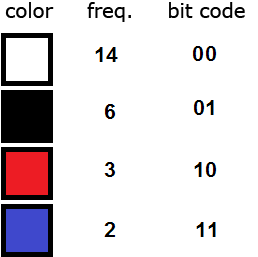
Using the variant is preferable in our example. This is because it provides better compression for our specific image.
Because each color has a unique bit code that is not a prefix of any other, the colors can be replaced by their bit codes in the image file. The most frequently occurring color, white, will be represented with just a single bit rather than 8 bits. Black will take two bits. Red and blue will take three. After these replacements are made, the 200-bit image will be compressed to 14 x 1 + 6 x 2 + 3 x 3 + 2 x 3 = 41 bits, which is about 5 bytes compared to 25 bytes in the original image.
Of course, to decode the image the compressed file must include the code table, which takes up some space. Each bit code derived from the Huffman tree unambiguously identifies a color, so the compression loses no information.
This compression technique is used broadly to encode music, images, and certain communication protocols. Typically, a variation of the algorithm is used for improved efficiency. The method described is generally part of general compression algorithms such as Flate-ZIP for images or FLAC for music.
Lossless JPEG compression uses the Huffman algorithm in its pure form. Lossless JPEG is common in medicine as part of the DICOM standard, which is supported by the major medical equipment manufacturers (for use in ultrasound machines, nuclear resonance imaging machines, MRI machines, and electron microscopes). Variations of the Lossless JPEG algorithm are also used in the RAW format, which is popular among photo enthusiasts because it saves data from a camera's image sensor without losing information.